
 |
EFFECTIVE SPILL |
The effective spill is a measure of the uniformity of the arrival times of
the beam particles. Typically an experiment has a deadtime, once a trigger has
occurred. Any particle that comes inside that deadtime will effectively be lost.
For a given number of particles N and a total spill length T, the
best one can do is a uniform distributiuon of particles, provided the deadtime
is shorter than T/N.
Deviations from uniformity can occur at high
frequencies (e.g. related to RF), medium frequencies (multiples of 50 Hz) or
slow variations over the spill, e.g. if the beam moves slowly over small
apertures. In that case the data-taking capability of the experiment may be
reduced as if the same number of particles N were arriving over a
shorther time, the so-called effective spill.
Ususally the effective spill is measured by taking the coincidence of a singles rate with a delayed copy of itself, as illustrated below:
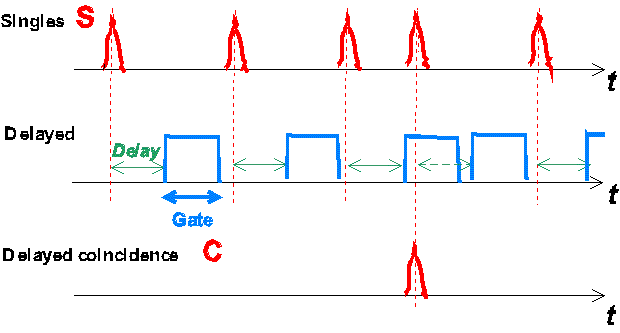
As one sees already in the figure, coincidences occur preferentially if the instantaneous singles rate is high. In fact the effective spill can be estimated as
And indeed one observes that the effective spill decreases when the
coincidence rate goes up.
The formula can be understood as follows:
The effective spill measurement of an experiment can be shown on page-1. The
experiment should provide two NIM signals into experimental scalers and define
the gate width. The EA physicists can declare the equipment numbers of the
scalers, using the p1spill interface (SingleSpill for the singles,
RateSpill for the delayed coincidence), as well as the Gate width in nsec.
Typical values of the effective spill range from 1.5 to 2.0 seconds for a
nominal spill length T of 2.38 seconds.